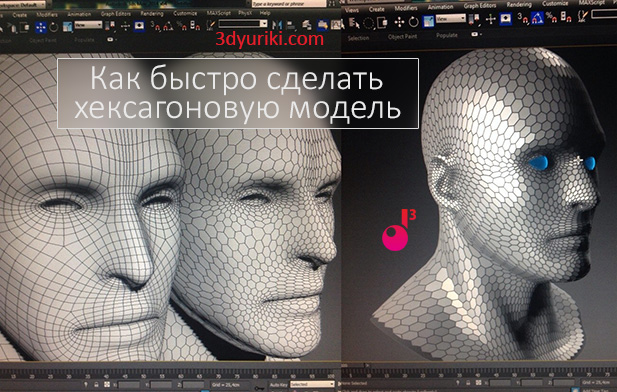
Хексагоновая модель - это та, которая состоит из шестиугольных полигонов, как пчелиные соты. Этот метод не идеальный (остаются кое-где семиугольники - в местах, где раньше были треугольники), но лучше, чем стандартный максовый.
Создавать топологию на основе шестиугольников мы будем в 3ds Max.
- Берем любую квадовую (состоящую из четырёхугольников) модель (я взял голову, как на заглавной картинке). Можно чтобы модель была и со звездочками (когда из одной вершинки выходит больше, чем 4 ребра) и с треугольниками. Главное чтоб n-гонов было минимум или не было вообще.
- Переходим в режим выделения полигонов, выбираем все, жмем Edit Triangulation и затем Retriangulate. Этот шаг можно пропустить если нет сомнений в однородности триангуляции.
- Не снимая выделения с поликов, идем в режим вертексов, выбираем все, жмем Connect и тем самым триангулируем модель.
- Не снимая выделения с вертексов, идем в режим поликов (все должны быть выделены с прошлого раза, если нет - выделяем), далее жмем Tesselate.
- Переключаемся обратно к вертексам и видим, что сейчас выделены все вертексы кроме новообразованных. Сразу жмем клавишу Backspace и получаем хексы.
Далее можно делать что душе угодно: инсерт (с последующей инверсией выделения и удаления промежуточных поликов), экструд, чамфер всех границ в затем и в конце турбосмус.
Подпишитесь на обновление блога (вот 3 причины для этого).
Спасибо за способ
Не по теме: я давно уже знаю, что для обучение практически любой профессии требуется всего 2 месяца. Вот, к примеру, оператор котельной - 2.5 месяца и вы с нуля обучаетесь новой специальности. И то, этого времени даже много. Только очень специфические профессии требуют 6 месяцев. Учтите, чтобы стать профи в любой профессии нужно 10000 часов посвятить ей.
Вам понравилась статья? Хотите отблагодарить автора? Расскажите о ней друзьям.
Или подпишитесь на обновление блога по E-Mail.
комментария 2 к статье “#26. Секреты 3ds Max: как быстро создать шестиугольную топологию для брони”
Извините, в данный момент комметарии закрыты.






Спасибо)
а у меня, почему-то шестиугольники стремятся к овалу, а не к окружности…